AIRPLANE FLIGHT ANALOGY
1997 William Beaty

This is a major mistake. The behavior of 3D wings is fundamentally different than the behavior of 2D airfoils. Going from 2D to 3D is not a trivial change.

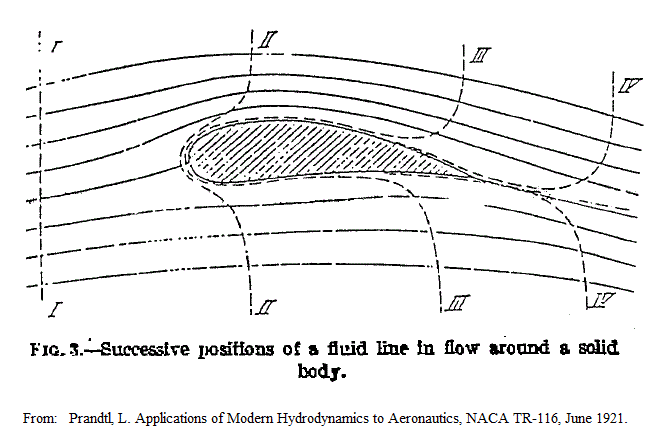
In our 3D world, airplanes behave like hovering helicopters, producing a downwards-moving plume of air. When flying horizontally, the plume of air becomes a downstream wake which carries away downwards momentum, and constitutes a net downwash. The wing injects downwards momentum into local air parcels, and this air keeps moving downward long after the aircraft has departed.

We encounter this as a wide, descending air mass commonly labeled "tip-vorticies."

But in the 2D world of the wind-tunnel, there is no such downward-moving wake behind the wing. Instead, the 2D upwash must always be exactly equal to the 2D downwash, and the wing does not push upon the air. Instead, all the momentum is injected directly and instantly into the distant floor/ceiling. Even more important, 3D wings have finite dimensions, while 2D wings act as if they have infinite span. An infinite wingspan gives some exceeding strange results; odd results never produced by finite 3D wings in the real world.

For example, if a 2D infinitely-wide wing should ever deflect even a tiny portion of the oncoming air downwards (deflecting a streamline,) it would deflect an infinite amount of air, and produce an infinite lifting force. As a result, a 2D infinite airfoil does an odd thing: it applies a finite force to an infinite mass of air. In response, a net amount of air does NOT move downwards (since it has infinite mass.) The incoming and outgoing streamlines remain horizontal. The wing doesn't deflect any air at all, on average. The wing acts like a weird reaction engine, a strange engine where the "exhaust gasses" have zero velocity and infinite mass. This strange effect only applies to 2D airfoils and to infinitely-wide wings, and obviously is never encountered with real 3D airplanes flying through 3D air.

In other words, flight of airplanes in the real world is an example of reaction engines and propulsion, same as with hovering helicopters and hovering rocket engines. Real wings are reaction engines. But the flight of a 2D airfoil is not propulsion, and doesn't inherently require any fuel. Real 3D airplanes require fuel, even when flying in an idealized zero-friction environment. (Real helicopters and rocket engines are the same. But a rocket engine with an infinitely-wide engine-bell does not need fuel and is not a reaction engine. The same is true of a helicopter with infinitely-wide rotor blades ...and true for a two-dimensional airfoil in a world of 2D streamlines.)

I attempt to explain the problem in words, but words are easily misunderstood (especially on hot-button issues where emotions run high.) A visual analogy works much better. Below is my explanation for how a three-dimensional airplane flies through 3D air. It is very different than the typical 2D explanations found in most textboooks. My "circulation" is flipped ninety degrees!

Take a look at my animated crude GIF diagram, and also see the green smoke laser-scanned video segment of a model 747 producing a downwash pattern.

                      _____
                   _--     --_
                  /           \
               __|      .      |
                 |             |
                  \_         _/
                    --_____--

Now suppose I were to leap from the top of a ladder and onto the balloon's small platform. The balloon would move downwards. It would also rotate rapidly counterclockwise, and I would be dumped off.

Next, suppose we have TWO giant disk-shaped balloons stacked adjacent to each other like pancakes standing on edge.

                     ____
                  _-- _____
                /  _--     --_
             __|  /           \
               __|      .      |
                 |             |
                  \_         _/
                    --_____--

Next, suppose we have a row of these disk-balloons one KM long. It looks like fig. 2 above, but with hundreds of hovering balloons. Now I can run from platform to platform, and I will stay aloft until I run out of balloons. Behind me I leave a trail of rotating, downward-moving balloons. I can remain suspended against gravity because I am flinging mass downwards. The mass takes the form of helium mass trapped inside the balloons. I am also doing much more work than necessary, since the energy I expend in rotating the balloons does not contribute to my fight against gravity. (In truth, all my work is really not necessary, I could simply walk along the Earth's surface with no need to move any massive gasbags!)

To make the situation more symmetrical, let me add a second row of platform-bearing balloons in parallel to the first row:

              _____                 _____
           _--     --_           _--     --_
          /           \         /           \
         |      .      |__   __|      .      |
         |             |       |             |  
          \_         _/         \_         _/
            --_____--             --_____--

Fig. 4 Forcing the balloons downwards

Also see: Smoke Ring animation

"DISK BALLOONS" BEHIND AIRPLANES

FLY FASTER FOR LESS DRAG?

Similarly, if a real aircraft flies slowly, it must fling the vortex-pairs violently downward. It performs extra work and experiences a very large "induced drag." If it flies fast, it spreads out the necessary momentum-shedding across a much larger volume of decending air, and therefore it needs only barely touch each mass-parcel (each "balloon.") Hence, faster flight is desirable because it requires far less work to be performed in moving the air downwards. And if a slowly-flying, heavily-loaded aircraft should fly very low over you, its powerful wake vortices will blow you over and put dust in your eyes.

All of my reasoning implies that modern aircraft actually remain aloft by vortex-shedding; by launching a long chain of combined "smoke rings" downwards. Imagine one of the flying cars in the old 'Jetsons' cartoon, the ones with those little white rings shooting down out of the underside. But rather than launching a great number of individual rings, modern aircraft throw just one very long ring downwards, and they are lifted by the upward reaction force.

L. PRANDTL, FATHER OF ...STUFF

First, if we analyze a 2D airfoil, we should find that the lift-force is equal and opposite to a downward force on a nearby solid surface. The system must include both the wing and the ground. If not, if we do like Prandtl and refuse to sketch in the ground surface, then we're creating a single-ended force which violates Newton's 3rd. Well, can't we move the ground far away? No, that doesn't work, since the force upon the ground is constant, and doesn't decrease with flight-altitude. (It's only permissible to remove something to infinite distance, if this reduces the pertinant variables to zero, and the force on the ground doesn't reduce.) The reason behind this phenomenon is interesting. A 2D airfoil is an infinitely-wide wing. Infinite span. It's forever trapped in ground-effect flight-mode, even if it flys at miles of altitude. (The span is inifinte, so in comparison, the wing is right next to the ground, even when miles high.) Whenever we explain a 2D airfoil, really we're explaining a "W.I.G." or wing-in-ground aircraft. A Caspian Sea Monster, those weird Russian planes with the ICBM nuke warheads. If a real airplane is like a hovering rocket, then a 2D airfoil is like a rocket with an infinitely-wide engine-bell. With a rocket motor, if we make the motor infinitely wide, then the exhaust-velocity decreases to zero, and no fuel is needed to create the thrust. It stops being a reaction engine. No propulsion, just a static thrust appearing from nowhere. In other words, a 2D airfoil, which is supposed to be like any airplane, was supposed to be a reaction-engine, but the infinite-wingspan effect screws up everything. (It causes an instant-force against the ground; a force which doesn't exist with real airplanes, except when those airplanes are flying at altitudes below about twenty feet!)

Prandtl does it again too. When working with 3D airfoils and their closed circle of vorticity (the tip-vortices, and the distant start-vortex,) Prandtl makes things simpler by analyzing horizontal tip-vortices. Big mistake. HUUUUGE! Having horizontal tip-vortices is the same as flying your aircraft faster and faster, and finally infinitely fast ...while attempting to remove the down-momentum being injected into the air. Unfortunately it doesn't work. The weight of the airplane is constant, so the rate of down-momentum injected into the air is constant. Speed of flight has no effect. If we try to remove this complicated momentum effect, by flying infinitely fast, by making the tip-vorticies horizontal, then again, we directly violate Newton, because flight-speed doesn't affect the net down-momentum! Again, a rocket-analogy. It's like having a rocket-engine where the exhaust-velocity is infinite. With infinite gas-velocity, then we dont' need any gas at all, and our rocket uses zero energy, zero fuel when producing thrust. (Wings as reaction engines are harder to analyze. So Prandtl just violates Newton, and declares that wings aren't based on propulsion, or creating any "exhaust plume," any momentum-bearing tip-vortices moving downwards.)

So, if you don't understand how wings work ...perhaps it's because real wings are reaction-motors, they're propulsion devices, same as hovering rocket engines (or hovering helicopters.) They work by pulling in air from all directions, then launching it downwards. But this involves changing vorticity, which brings in the horrible mathematics of turbulence. To avoid this, to make the equations have actual solutions, Prandtl cheated. He accepted the fundamental Newton-violations, in pursuit of simple math models. But then he crossed the line, because he never explicitly stated that this is what he was doing, or admitted that his models were completely un-physical (flagrantly violating simple Newtonian physics.)

OK, enough Prandtl-bashing. I'll let others take up the big club and have a go at him. (I'm thinking, he deserves it.)

A CRUDE PREDICTION

Suppose the "disk-balloons" contain air which rotates as a solid object, (or imagine radial membranes in the balloons. Or stuff them with aerogel.) If I then add together the work done in creating the circulatory flow, plus the work done in projecting the constrained air downwards, I arrive at a predicted aircraft power expenditure of:

Power = 8 * (M * g)^2 / [ pi * span^2 * V * density ]

Induced Drag = 8 * (M * g)^2 / [ pi * span^2 * V^2 * density ]

How does this match reality? I'm looking for information on this at the moment. I'm told that these two equations are identical to the equations of real aircraft, except that the number "8" is replaced by a factor which is dependent upon the particular geometry of the wing. So, calculated from first principles, without prior instruction in fluid dynamics. Pretty good for an "amateur aerodynamicist", eh?

One final note. The downwash vortices of real airplanes contains rapidly rotating air. This represents wasted energy, since only the "shell" of each "balloon" needs to rotate as the region of air moves downwards. Is there a wing which can produce a downwash vortex-pair without any spinning cores? Maybe it would use less fuel than modern wings.