SCIENCE HOBBYIST  |
K-6 MISCONCEPTIONS  |
GOOD STUFF  |
NEW STUFF  |
SEARCH
 

Lasers: What is Coherent Light?
A bad K6 textbook diagram, and a widespread misconception
William Beaty 2004

Laser light behaves very differently than light from other sources. Books aimed at children and the general public give two reasons for this:
  1. Laser light is monochromatic or very pure in color.
  2. Laser light is coherent light, or special "in-phase" light.
What does "coherent" mean?

As a kid I was always confused by explanations of coherent light. I'd been told that coherence had something to do with the sinusoidal shape of photons. Light is supposedly made up of little wiggling string-shapes; transverse waves. Textbooks show each photon as a kind of little "snake" moving side to side. And, supposedly, whenever all the "snakes" pack together side by side with their wiggles aligned, that's Coherence. Atoms in a laser are all emitting their light in phase-lock, and supposedly the end result is a special kind of "Inphase Light," where the little sine-waves stack up together, much like egg cartons.

But somehow this explanation just wouldn't stick to my brain. It didn't fit with everything else I knew. And worse still, I couldn't use the explanation as a tool. On one hand, the typical explanation of monochromatic laser light was very useful in many situations. Pure color means single frequency, and that implies narrow peaks in the spectrum graphs, and tiny spots on the radio dial. "Monochromatic light" connects with audio, where the pure tones such as flute-notes are monochromatic, while an impure broad-spectrum tone sounds like pink noise (or perhaps violins.) And in holography, whenever the frequency of light is moved high or low, I could imagine how this would slide all those tiny diffraction patterns around on my film. That would blur the patterns and make holography impossible, so clearly a hologram camera needs a very monochromatic light source. As a concept, "Monochromatic" works!

So where is the equivalent power in the concept of "coherence?" How do I use those stacked-snakes to explain many other things? Where do the parallel wiggles clarify a radio antenna, a loudspeaker, or water waves? And if my laser isn't coherent enough to make holograms, can I draw a very simple picture of the problem's exact nature? A simple picture that any kid could understand? No. It just didn't connect.

Well, after a few years in the physics business I did figure it out. Jeeze, I just shoulda known...

That explanation is WRONG.
The explanation of Coherent Light found in most K12 introductory textbooks is pure garbage. It's worse than just wrong. It gave me a mental barrier. It led me directly into misconceptions, and I couldn't go forward until I'd un-learned them again.

To get right down to it, light isn't a transverse wave. Or more specifically, light isn't a "transverse wave in the Aether," instead light is a wave in magnetic and electric fields where the field vectors point sideways. But the flux lines themselves don't wiggle sideways, and the flux doesn't contain any sine-wave shapes. Take a look at the video below left. The animated graph depicts the field strengths found along a single straight line: the values of the fields when a light wave is passing towards the right. The only sinewaves present are found in the pattern of intensity, in the sine-graph of field strength measurements. That sine wave is not a flux shape in space. In that vid, the only space involved is a straight-line axis with no wiggles.
ads:
EM field strengths graphed along a straight line.
(*NOT* a plot of flux lines.)

The expanding onion: flux lines surrounding a tiny light source. No wiggling snakes in the field structure.

 

If we could see light and radio waves, could we find any little sinewave-snakes anywhere? Nope. Take a look at the second video above right. It shows what EM waves would actually look like, if we could see them. It's an animation of flux lines surrounding a very tiny light source. The EM waves expand like layers of an onion. The flux lines break loose from the source, close upon themselves to form loops, then fly off into space. Of course if we graphed the field strengths on a voltage axis, they would form sine waves, as shown in the first video. But the flux itself isn't like a snake. It points entirely sideways all the time, like closed rings with no sine wiggles. And of course there isn't any "Aether medium" which could wiggle like transverse sine waves. No little snakes flying through space. Like atoms being little solar systems, the wiggles were "lies to children." Or, they were simply wrong.

And photons? ...the photons are either dimensionless particles, or they're broad wavefunctions which are 'quantized.' They're either like infinitely small bullets flying in straight lines, or they're like enormous expanding EM pond-ripples from a thrown pebble. Photons aren't shaped like twisty snakes, they're nothing like a transverse wave on a string.

In other words, the entire crazy "stacked wiggles" explanation of Coherent Light falls apart.

And even more important than all of the above... I realized that the in-phase emissions in lasers don't even create any "in-phase light" in the first place! [It's important enough to say twice: coherent light isn't created by in-phase stimulated emission. That's a big one.] In-phase emissions are important of course. But they only cause light amplification. They create amplified, brighter light. So what creates the coherence? I'll get to that, but first more about the error.

Whenever atoms in a laser are emitting EM waves in phase with incoming EM waves, the emitted waves add to the incoming light, making it brighter. Two plus two equals four. But amplification doesn't create any "in phase light." If two plus two is four, the resulting 4 is purely a number, and it isn't concealing any 2 + 2. Instead it could be one plus three, or nine minus five. I mean, when two in-phase waves add together to create an amplified wave, the original waves are gone. The larger wave doesn't forever travel along as two smaller "inphase waves" in the way all those intro laser explanations depict. Instead, all those diagrams should show that smaller waves add together to create single, larger waves. Amplification. Not some sort of "coherence-izing effect."

 

THE BAD DIAGRAM

The laser's in-phase emission arises in other topics: it's the basis for transparency of materials. For example, whenever atoms in a glass window absorb light waves, they re-emit those waves in phase, so the original wave is preserved and the material acts transparent. In-phase emission prevents the light from scattering when it interacts with the atoms in the glass. So yes, the atoms in the laser-rod or laser gas-tube emit light in phase... making the laser material transparent, and this preserves whatever coherence that the incoming light might already have had. The "in phase" textbook laser diagram below is actually, heh, explaining transparency. Incoherent light could also get amplified and bounce as shown below. So, the authors never bothered to tell us how the light became coherent in the first place.

 
THIS IS WRONG. LASERS DON'T WORK LIKE THAT.
Fig. 1 The bad diagram. Did you learn this one in school? If so,
you may need to un-learn it before you can understand coherence.
Coherent light does not behave anything like this.

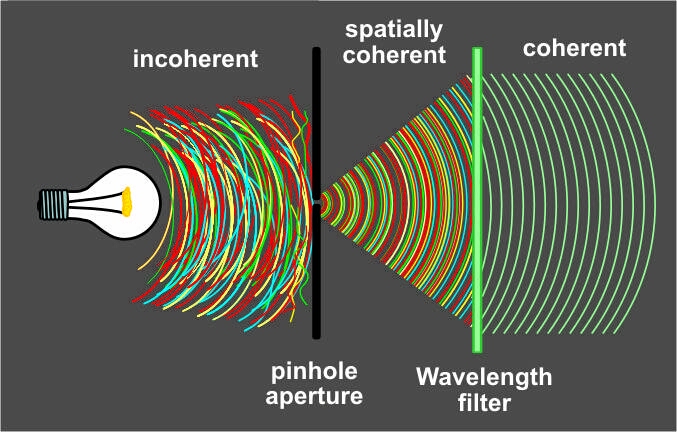
If fig. 1 above is wrong, then what's right? If we could actually see individual light waves, what would coherent light look like? Fortunately the explanation is quite simple. Take a look at figure 2A below. That's what perfectly coherent light would look like if we could see the waves. Coherent light is simple: it's light which comes from a very small light source. Light from a single source is always coherent, since incoherence requires two sources. Spatially coherent light has another name: "sphere waves" or "plane waves." Or even simpler: "pinhole light" or "pointsource light."

[tiny dot sends out a bullseye shape of red waves]
[tiny dot sends out a sunburst of red rays]
A. B.

Fig. 2  A coherent light source emits waves and/or particles.
A perfectly coherent source is just a point-source.

A single small light source sends out electromagnetic waves in all directions as shown above. Of course these diagrams are only two-dimensional, while the real situation is 3D. We can visualize a coherent wavefront to be spherical. The waves are like layers of a spherical onion, but where the onion is expanding at the speed of light, with new layers constantly added in the center. OR... we could imagine that the tiny light source is sending out a stream of particles flying off in all directions. The paths of these particles are the "rays" of light. Since they all fly outwards from a single point, none of the rays cross each other. And if this light is passed through a converging lens, it's focused to a perfect point.

Coherent light is just some:

  • Rays which never cross each other; parallel or radial
  • Perfect wavetrains in 3D; nested sphere-waves or plane-waves

So coherent light is just "pointsource light?" Paraphrasing Feynman: Now I Understand Evvvvvrrreeethiiing! Finally it all makes perfect sense: starlight is ULTIMATELY coherent, that's why Stellar Interferometry works. Starlight has coherence-lengths in thousands of KM, starlight is far more coherent than any human-made laser light. And the most distant stars are just like ideal point sources. I remember AA Michelson discovering that Betlegeuse is far less coherent than other stars. Ha, far less like a microscopic pointsource! Then I suddenly remember Dennis Gabor, inventing holography before lasers existed. To create his pseudo-lasers he just took light from an ordinary mercury-arc lamp and passed it through a pinhole. Mercury's emission line made it nearly monochromatic, and the pinhole gave it the spatial coherence.

Pinhole pinhole, ever hear of an optics device called a "Spatial Filter?" They're used to 'clean up' laser light and make it much more spatially coherent. A Spatial Filter is just a very small pinhole with a converging lens upstream: any "incoherent" parts of the beam will never make it through the tiny aperture. It restores an imperfect laser's point-sourcey-ness.

And finally I know why lasers are so wonderful: lasers are pinhole light sources which are ...actually bright! It's always been easy to make some coherent light, just use a normal light source and an optically small pinhole (a halfwave diameter.) A frosted light bulb can become a coherent light source. But a pinhole aperture this small will block nearly all the light from any conventional source. To experiment with this, get a slide projector and make a slide with a pinhole: an Al foil layer perforated by a needle. Add a narrowband green filter, and that's your Gabor-approved 1940s laser source. Make some holograms? Heh, a bit long exposure-time though.


 
Fig. 3 SOMEONE GETS IT RIGHT! The above
unattributed diagram found in online archives.

In the distant past, monochromatic coherent sources were also microwatt light sources, no getting around it. Creating coherent light meant throwing away almost all of the power. Sending many milliwatts of light through a wavelength-diameter pinhole was basically impossible. So, all the bizarre and wonderful capabilities of lasers were unreachable.

But lasers easily solved the problem because, right at the start, they create some spherewave "pinhole light," as if their entire light output came from a single virtual pinhole; a pinhole which is less than 500nM across. Aha, those confocal/concentric resonator mirrors, the ones used in lasers? This means that the "virtual pinhole" in an actual laser is just a non-virtual, very real pinhole-image sitting in the space between the mirrors. (See wikipedia diagrams for optical cavities, http://en.wikipedia.org/wiki/Optical_cavity). And all of those Semiconductor Lasers with parallel mirrors: they just employ an "infinite mirror tunnel" in order to place their pointsource at virtual-infinity distance, where it behaves just like the light from a distant star. During its trip down the infinite tunnel, all the non-planewave light wanders out the sides of the tunnel. Only planewave light can persist in the tunnel and get amplified.

So ...laser coherence is created by the mirror-tunnel. Not by transparency or stimulated emission or 'stacked sinewaves." Or in proper terms, coherence is created by the laser's Fabry-Perot resonator cavity, and not by any sideways packing of long narrow string-like "photons."

And all the above means that we now have a simple, gut-level intuitive picture of laser coherence. What is it? Coherent laser light is just pinhole-light produced by an infinite mirror-tunnel, with amplification. Sort of like those disco-era mirror-infinity toys from Spencer Gifts. But the depths of their virtual tunnel wouldn't be dark. On each reflection, the light passes through the laser-medium and gets slightly brighter. And on each pass, the "virtual source" seems farther away inside the tunnel. Viewed from the end, each deeper segment of the "tunnel" appears slightly brighter and smaller ...and the far end of the tunnel looks like an infinitely bright, infinitely tiny star. If you stare into the depths of the Amplifying Disco Infinity Mirror, the "star" is small and bright enough to punch a hole right through your retina. And it doesn't even have to be very bright to do this! A hundred-watt incandescent light bulb doesn't slice up your retina, but a quarter-watt laser can burn a tattoo permanently into the back of your eye. "Coherent" can also mean "sharp when focused," since focused Coherent light must all converge to an infinitely small point. (Yeah yeah diffraction limit. We're talking simple idealized geometrical optics here.)

OK, if spatially coherent light looks like an expanding bullseye, then what does INCOHERENT light look like? In the above diagram 2A, incoherence instead would look like multiple pinholes and bunches of overlapped bullseyes. Lots of interference patterns, and probably with the nodes dynamically swerving around. Either that or it would look like fig. 2b but with bunches of light rays from multiple pinholes, and the rays all cross each other throughout the light beam. In both cases if the incorherent light was focused by a lens, we wouldn't produce any infinitely tiny hot spot. Can't punch holes in razor blades.

With our gut-level intuitive understanding of Laser Coherence, we can now construct a basic list of coherent light sources

Sources in increasing coherence

  • Bright cloudy sky (least spatially coherent)
  • Fluorescent tube lamp
  • Frosted incandescent bulb
  • Sun during clear weather
  • Clear incandescent bulb
  • Clear incandescent bulb w/noncoil filament (aquarium bulb)
  • LED
  • Electric welding arc 50ft away
  • Laser (coherence-leng in MMs, up to a few Meters)
  • Starlight (coherence leng 1000s KM)
Note that the list also is a list of DEcreasing visible source-width, with the cloudy sky at the top and the distant stars at the bottom.

As a little kid, did you believe that the light from clear incandescent bulbs was more magical than the frosted ones? And the light of garage welders was even more magical still? If so, you were intuitively experiencing optical coherence. Your little brain was wanting to mess around with laser sources, rather than overcast daylight.

A perfect ideal pointsource gives perfectly coherent light, while a wide diffuse source gives the least coherent light. Turn the idea backwards: if we start out with perfectly coherent laser light, but then we send it through a frosted screen, the light remains just as monochromatic, but it becomes incoherent. Hey, I noticed that we can actually buy an incoherent-izer, an opto device for our optical bench. They're just a rotating frosted screen with a little motor (since an unmoving frosted screen still leaves a small bit of micro-scale coherence or "laser speckle.")

NO JPEG YET

Fig. 4 A frosted screen makes light incoherent.

REAL SOLAR DEATH-RAY

And now I have the answer to a big question that plagued me in childhood. No doubt all the nasty little science-boys like me had come up with this one. Why can't I make a death ray light-source? I could just get my big plastic fresnel lens and focus sunlight, and then somehow collimate it into a half-mm beam. The 0.50mm burning spot would appear anywhere along the parallel beam miles long. Write CHAIRFACE on the freakin' moon! But if we think about this now, it turns out to be impossible. Adding extra lenses to our solar furnace just creates a projector, where our parallel solar deathray spreads out and becomes a wide image of the sun. The darned sun isn't a pointsource. No thin beam is possible unless we include a tenth-micron pinhole in the optical path, and that turns the power into microwatts. The solution to the problem is simple: JUST REPLACE THE SUN WITH A 10KM WHITE DWARF STAR HA HAAAA! Keep the sun's brightness the same, but shrink the sun until it appears in the sky like a tiny star, like an extremely intense pinpoint. Now just use any big lens to gather a square meter of sunlight, focus it down to 1mm, then collimate it with a 1mm water-cooled short-focus quartz lens stolen from an ultraviolet microscope. Yes, the whole device is still a projector, but if we project the image of a pointsource into the distance, the result is an intense collimated beam. Other than a bit of diffraction it should work great: a few hundred watts in a parallel CW beam 1mm wide. Slice-a offs you fingas!

Winston Kock, one of the early laser people at Bell Labs, said that laser light is "sharper light" which can be used as a cutting tool. Exactly, exactly! Winston Kock actually gets it. But the actual central concept is that coherence or "pinhole light" is the whole reason for the "sharp light" which does the laser-cutting. Lasers aren't particularly bright. Hundred watt light bulbs? 5,000 watt spotlights for school play?? Or daytime sunlight? If our sun was 10KM wide, or reduced to 10^5 times smaller in visual angle, then its light would be spatially coherent like lasers, or like an electric welding arc, and glancing upwards during the day might slice grooves across our retinas. The lens of your eye will focus the white-dwarf sunlight to a pinpoint rather than to a dim and safe little 0.3deg solar disk on your retina. Only because sunlight is non-parallel, because our sun is an extended source, our 1.5 KWatt/m^2 sunlight doesn't act like dangerous laser light. Hmmm, hold on a sec. If sunlight is about 1500 watts per square meter, and your eye's pupil is about 1mm, then your pupil intercepts 1500W/.001^2 = 1.5mW. DOH! WRONG! OK, staring at white-dwarf sunlight would actually be just like staring into a cheap laser pointer. Those things don't become really dangerous to human eyes until up around 5mW. AHA, but using binoculars would be bad, very bad: 5000X smaller exit aperture, creating an eight watt parallel beam 1mm in diameter. Binoculars become like icepicks aimed at your eyeballs. Coherent light can be nasty.

See LINKS below


ADDENDUM: General mathematical theory of EM partial coherence

If you read the first paragraphs here, you'd know that this article only describes Spatial Coherence, not temporal coherence or monochromatic light. (Important! Don't miss it.)

Also, this article is aimed at the general public as well as grade-school teachers and students. So, no math whatsoever! Also, this article explains IDEAL coherence: light with perfect spatial coherence.

On the other hand, Partial spatial coherence is a whole 'nother kettle of fish, and is nearly impenetrable without recourse to algebra and trig. Even further: the mathematical "coherence" concept in general; the mixture of spatial and temporal coherence ...is not mentioned anywhere here.

Instead I'm following the usual distinction made by the intro textbooks. In these books, perfectly coherent light is explained separately from perfectly monochromatic light (i.e., spatial coherence is not temporal coherence.) Here I'm ignoring single-frequency waves, and only explaining the ideal pinhole-light, white light from wavelength-size apertures. Also, I'm not treating light from extended apertures. I'm explaining the light from distant stars, not the light from nearby Betelgeuse.

In other words, where kids and the public are concerned, the term "coherent light" has a distinct meaning. It does not mean generalized coherence. Instead, for the greater public, "coherent light" means "light of perfect spatial-coherence," such as white light from ideal pinholes. But at the university level things are very different, where the term "Coherence" means a general theory; a mathematical description of non-ideal partial coherence which combines monochromatic light with the light from non-pinhole extended sources. A general theory of coherence does not divide temporal coherence from spatial.

Do "textbooks" get Coherence completely wrong? Yes: grade-school textbooks, K-12 textbooks. Also articles written for public consumption, they get it wrong too. But the college textbooks, they're fine. They go into the rigorous details of partial coherence, and mixtures of spatial and temporal coherence, and they don't teach us that photons are like little sine-waves which can pack together like cardboard egg-cartons.

SEE ALSO:

Common Laser Misconceptions

Electricity misconceptions
http://amasci.com/miscon/coherenc.html
Created and maintained by Bill Beaty. Mail me at: .
View My Stats