
SQUARE WHEELS
1999 William Beaty
Imagine a solid cube. Inflate it a bit so it has a slight "pincusion"
shape. Now drill a hole through it, through one pair of diagonal
vertices. Stick two of these pincusioned-cubes on an axle. If the
elliptical curves of the "pincusioned" edges are correct, then this
device will roll perfectly smoothly, like a glass ball. Square wheels!
Or, recall that if you view a cube along its diagonal vertices, you see a
hexagon. If you bend the edges of the cube outwards a little, then the
hexagon becomes a circle. Circles can roll!
Or, imagine the volume which is created by the intersection of four
cylinders passing through a central point. Now grind the pointed pyramids
of this volume down, leaving only the "cube" edges. The result looks like
a slightly-swollen cube. The edges are segments of ellipses. This cube
can roll, if placed upon an axle.
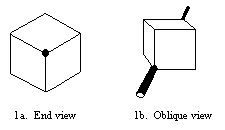
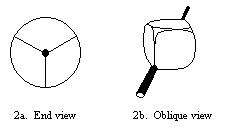
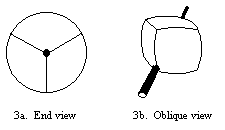
In 1991 we had an RC car from Radio Shack with four polished plexiglass
"square wheels" zooming around the lab. A pair of "square wheels" on an
axle makes a great physics-paperweight. Triangular wheels look even stranger.
I wonder, was this my independent invention? Or is it already well known?
I've never stumbled across any papers on "square wheels" since I started
playing with them in 1991. I wouldn't be suprised if there was some obscure
article about them in a journal somewhere.
Similar things can be done with a tetrahedron (triangular wheels), or
most any polyhedron.
I came up with this while trying to think of some cool "science toy" to
top Piet Hein's "Superegg". Square wheels is actually just a ripoff of
the Exploratorium exhibit where thin inflated triangles are used as roller
bearings (the edges of the triangle are segments of a circle, with center
of curvature placed at the vertex opposite each side). Not a big leap
from an inflated triangle to a rolling cube, eh? :)
- Constant-width shapes
- Square wheels on catenary road
- Reuleaux Triangle
- more Reuleaux
- Here's something similar: Reuleaux Tetrahedron
- Cubical business cards