Another situation is a bit, less misleading: think of the word "charge" as
applied to gunpowder. A charge is placed in an old cannon, followed by a
cannonball. It would be silly to assume that, because we've "charged" the
cannon, the cannon now has an electrical charge. Yet whenever we state
that we've "charged" a capacitor, we do assume that an electrical
charge has been stored inside. This is just as silly as mistaking
gunpowder for electrostatic charges. Charging a capacitor (or a battery)
is like charging a cannon; in both situations we are inserting energy, not
electrical charge.
Here's yet another way to visualize it. Whenever we "charge" a capacitor,
the path for current is through the capacitor and back out again. The
extra electrons on one plate force electrons to leave the other plate, and
vice versa. Visualize a capacitor as being like a belt-driven wind-up
motor. If we shove the rubber belt along, the spring-motor inside the
capacitor winds up. If next we let the rubber belt go free, the wound-up
spring inside the motor drives the belt backwards, and the
spring becomes "discharged." But no quantity of "belt" is stored inside
this motor. The belt flows through the device, and we wouldn't
want to label
this motor as a "machine which accumulates rubber." Yet this is exactly
what we're saying whenever we state that capacitors "store charge."
One more try. Capacitors store charge in the same way that resistors
store charge, and inductors store charge. Inductors are full of mobile
electrons, inductors are devices for storing charge!!!! Nope. An
inductor isn't a bucket for accumulating electrons, and neither is a
capacitor. Instead, both types of component behave like piece of wire
But capaictors are magical wires which, whenever we run a
current along it, the total charge inside the wire stays constant, but a
voltage (and a charge imbalance) appears at the two ends.
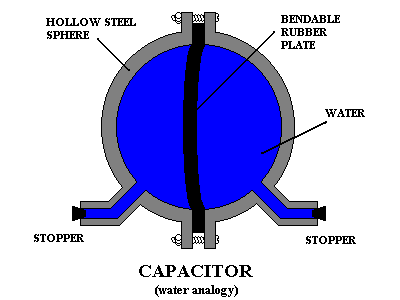
My favorite capacitor analogy is a heavy hollow sphere which is
completely full of water and is divided in half with a flexible rubber
plate through its middle. Hoses are connected to the two halves of the
thick irong sphere, and they act as connecting wires. The rubber plate
is an
analogy for the dielectric. The two regions of water symbolize the
capacitor plates.
Imagine that the rubber plate is flat and undistorted at the start. If I
connect a pump to the two hoses and turn it on for a moment, the pump will
pull water from one half of the iron sphere and simultaneously force it
into the other. This will bend the rubber divider plate more and more.
The more the plate bends, the higher the back-pressure the plate exerts,
and finally the pressure-diff will grow strong enough that the pump will
stall. Next I seal off the hose connections and remove the pump. I now
have created a "charged" hydraulic capacitor.
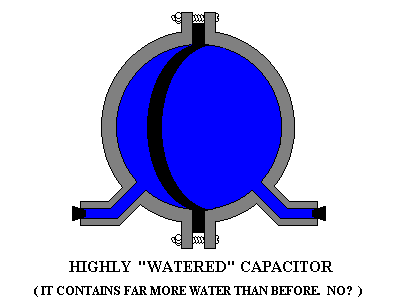
Now think: in this analogy, water corresponds to electric charge. How
much water have I put into my iron sphere? None! The sphere started out
full, and for every bit of water that I took out of one side, I put an
equal amount into the other at the same time. Same as when running a
current through a conductor. When the pump pushed water into one side,
this extra water also forced some water out of the other side.
No water passed through the rubber, instead there was some rubber-current
in the divide. Even so, essentially I drove a water
current through my hydraulic capacitor, and this current pushed on the
rubber plate and bent it sideways. Where is the energy stored? Not
in the water, but in the potential energy of the stretched rubber plate.
The rubber plate is an analogy to the electrostatic field in the
dielectric of a real capacitor.
It would be misleading to say "this iron sphere is a device for
accumulating water." And neither say "this sphere can be charged with
water, and the
stored water can be retrieved during discharge." Both statements are
wrong. No water was injected into the sphere while it was being
"charged." (And when I wind up an old watch, am I "storing steel"
inside it, putting more iron into its spring? Lol.
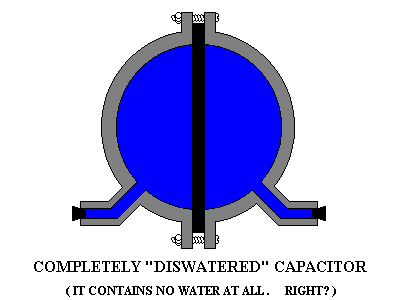
Imagine that I now connect a single length of pre-filled hose between the
two halves of my "energized" water sphere. As soon as the last connection
is complete,
the bent rubber plate will drive a sudden
immense
spurt of water through this already-full hose. Water from one side will
be pushed into the other side, and the rubber plate will relax. I've
discharged my hydraulic capacitor. How much water has been removed from
the sphere? None! A momentary current has flowed through the sphere
device, and the rubber plate is back to the middle again, and the water
has become a bit warm through friction against the surfaces of the hose.
The stored energy has been "discharged," but no water has escaped. The
hydraulic capacitor has lost its energy, but still contains the same
amount of water.
I never really understood capacitors until I started trying to construct
proper water-analogies for them. Then I discovered that my electronics
and physics classes had sent me down a dead-end path with their garbage
about "capacitors store electric charge." Since my discovery, I've gained
significantly more expertise in circuit design, which leads me to a sad
thought. Maybe the more skilled of electrical engineers and scientists
gain their extreme expertise not through classroom learning.
Instead they gain expertise in spite of our K-12 classroom learning.
Maybe the experts are experts only because they have fought free of the
wrong parts of grade school science, while the rest of us are still living
under the yoke of the many physics misconceptions we were carefully taught
in early grades.
[Hey, M. Steinberg's
C.A.S.T.L.E. electricity curriculum uses the same analogy! In all my
search of textbooks, this is the only one I've found. In
section 3.9, students construct a
2-chambered air capacitor with a balloon membrane stretched between the
two chambers. To "charge" it we take air from one side and pump it into
the other. ]
[Hey^2!!! I just found that Oliver Lodge was building mechanical
analogies for Maxwell's descriptions of EM fields and circuits... and for
an 1880 lecture he
built a capacitor hydraulic analogy consisting of a water-filled sphere
with rubber! His was a glass sphere containing a smaller balloon,
both full of water with no bubbles.]
LINKS
Extra notes:
Capacitors store just as much charge as coils do! In both devices the
total amount of charge stays constant. Whenever we force charge into the
first capacitor plate, equal charge must flow out of the second
capacitor plate. The path for current is through. Capacitors
and
inductors are both components for storing electromagnetic energy. They're
two
sides of the same EM phenomenon: a coil stores energy in a volume
containing a magnetic field, while a capacitor does something similar
with electric fields. Coils are "discharged" by interrupting a large
current and collapsing the b-field, while capactors are discharged by
shorting-out a large voltage and collapsing the e-field. Neither stores
any "electricity" (unless by the word 'electricity' you mean
magnetic field?) Of course we can place a coil atop an insulating
platform, then use a VandeGraaff generator to give your coil a large
net-charge! You can do the same with a big electrolytic capacitor too.
:)
Bill Beaty here again. Two points:
First, the heated topic about currents
being impossible between capacitor plates ...seems to be about
Vacuum Capacitors, not capacitors in general. Modern
capacitors are quite
different than vacuum capacitors, where inside a modern dielectric we'll
find a
large electron-current. Relative Permittivity can be seen as a ratio
between the small Maxwell's displacement current inside a vacuum,
versus the larger polarization current (electron flow:
the shifting of electrons) in the ferroelectric PZT material. The
dielectric constant in modern ceramic capacitors is above 2,000, so the
vast majority of the current in the dielectric is a genuine charge-flow, a
real current caused by
shifting the electrons in the ferroelectric
ceramic. The Maxwell displacement current
of the vacuum is insignificant: well below 1%.
Second: it might help to ask whether, down at the micro level inside
a metal, in the space BETWEEN the electrons, is there any electric
current? If there is, that's a current in empty space. And in that case,
there's certainly a current in the space between the metal plates of a
vacuum capacitor. Or said differently: if we have a current-sensor, and a
charged particle approaches and passes it, does our sensor indicate an
extremely brief pulse, where the pulse-width is associated with the
diameter of the charged particle? Or instead does our sensor see each
moving particle as being very large and "fuzzy," so that the measured
current is found in the fields surrounding each particle, and the current
extends forwards and back from the particle location? A clamp-on current
meter (Rogowski coil) doesn't detect the actual particles or their
motions. Instead it detects changing flux-linkage. It thinks that
amperes are made out of fields. A clamp-on sensor would report that each
charged particle is indeed large and fuzzy, and the current exists in the
empty spaces between the flowing charges. Current is not only found on
the flowing particles' surfaces where the moving charge actually resides.
So, a clamp-on sensor would 'see' currents in a vacuum-capacitor's empty
gap. The changing fields are in that gap, so that's where the current
appears.
Only two points? Third point, suppose we construct a capacitor
where the dielectric takes the form of a long rod: much thicker than the
diameter of
capacitor plates. Use a long narrow PZT lead-zirconate-
titanate rod with tiny capacitor plates attached to its circular ends.
Now apply some 27MHz amperes. Do you still insist that the current within
this
rod is zero? Really? It's not. Next, suppose we obtain a coil-shaped
spiral
rod of PZT. A ceramic "ferroelectric coil." If we apply some RF amperes
through
this spiralled dielectric, we'll certainly detect a strong magnetic field
surrounding the device. Our capacitor's dielectric is now a coil. If the
current is supposedly zero within all
capacitor dielectrics (as some people angrily insist,) how can we explain
this? Simple: capacitor dielectrics do contain current after all. The
value of current in the dielectric is exactly the same as the amperes in
the capacitor leads.