Are they REALLY holograms?

(No, scratch-holograms are not stereo pairs. The main website contains a stereo photograph of a working scratch-hologram of a glowing cube. If you want to see a true scratch-hologram in full 3D, you'll have to make one yourself.)

First of all, be aware that a diffraction grating does not function exclusively by optical interference. In addition to acting as diffractors, all diffraction gratings are also arrays of parallel line-scatterers. Because the line-scatterers (the diffraction fringes) are spaced equally, only light scattered from certain angles is reinforced while light from all other angles is eliminated. But because the fringes are line-scatters, their orientation determines the angle of deflection of the diffracted beams. If it did not, then gratings would diffract light into a cone rather than into a pair of 1st-order beams. (This of course is obvious, but it's so obvious that we might overlook it!)

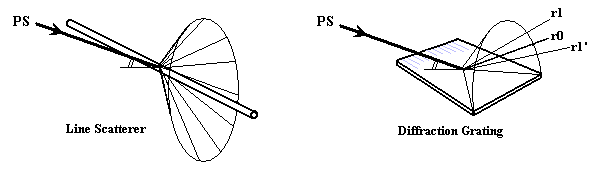
Here's another way to say it. A diffraction grating can bend light with TWO angles. One angle depends on diffraction. The other angle depends on grating rotation: it depends only on the angle of the lines in the grating with respect to the incoming light.

If we change the spacing of the grating's fringes, we can change the path of the diffracted light, but if we ROTATE the entire grating without otherwise modifying it, we also change the path of the diffracted light. Holography is not based exclusively on diffraction-bent light. In fact it relies on TWO effects: the angle produced by diffraction, and also the angle of the deflection-vector which is perpendicular to the diffraction. Some types of holograms (Rainbow holograms) rely only on the optics of line-scatterers for 3D depth effects. They rely ONLY on the rotation angle of the gratings in the recorded zoneplates, and the spacing of the fringes is not critical. That's why Rainbow holograms can still create images even when illuminated by white light. This is very different from conventional or "off-axis" holograms. The zoneplates of conventional holograms harness both the diffraction and the "line-scatterer" effects in order to create images. For this reason they require a monochromatic light source.

Here's why I call these images "holograms"

• Points on object are recorded on film as "zoneplates" which focus light.
• Illuminator must be spatially coherent (i.e. pointsource)
• Extended-source illumination produces same blur as in Rainbow holos.
• Conjugate illumination produces pseudoscopic (inside-out) images.
• Scratches are simplified versions of conic-section interference fringes.
• Wide regions of scratch-holograms contain entire images.

Fig. 1 The basic 'pixel' of a Rainbow hologram

In reality the little lines are thousandths of a mm apart. For an illuminator at infinite, the lines are smooth parabolas with a sinusoidal density profile.

The lines are microscopic. However the entire "swatch" of interference fringes on the film plane might be several mm wide and a fraction of a mm tall. It's similar to a small slice of the bullseye pattern in a Gabor zoneplate lens. During production of a hologram, the many individual points on the recorded object become little horizontal swatches of interference fringes on the film. The long rectangular profile of the above "swatch" is produced by the slit aperture used in the one-step rainbow hologram process.

Imagine that a Rainbow hologram is made up of thousands of these "pixels" laid atop each other. The X,Y position of each "pixel" corresponds to the X,Y position of each object point. For example, if you could stamp the above interference pattern in many places on your film, you'd have a hologram of a field of stars (but where each star has the same virtual depth within the film plane.)

The depth information for each image point is encoded as the overall size of the "single pixel" interference pattern: an image-point which reconstructs as being deep within the hologram will have a "pixel" with a large width and with long-radius, slightly-curved fringes, while a shallow point will have a tiny "pixel" and small-radius fringes. So a Rainbow hologram is very similar to a standard 2D photograph in structure, but instead of pointlike pixels, it has various sizes of swatches of interference fringes which store the depth info for each recorded point.

The above crude figure implies something interesting: depth information is only stored in the ANGLES OF THE SMALL FRINGES, and not in their spacing. If we observe a Rainbow hologram under laser light and under sunlight, we find that both types of light will reproduce the holographic image, but the sunlight creates rainbows. The hologram's fringes cause the diffracted image of the sun to be spread into a stripe of rainbow colors which will be seen as a virtual image within the horizontal "stripe-window" comprising each "single-pixel" fringe pattern. Other than this rainbow-colored artifact, the holographic image is not strongly affected by changes in illumination frequency.

A rainbow hologram, within limits, is a frequency independent hologram.

Frequency independence implies size independence (size being the spacing between interference fringes on the film plane.) In other words, if the Rainbow Hologram operates correctly with a wide variety of illumination frequencies, then the Rainbow Hologram should also operate correctly with a wide variety of fringe spacings. We could give the fringes random spacing and the hologram would still work. We could increase the fringe spacing, so higher order diffraction invaded the images... and the hologram would still work. Changes to the fringe spacing only affect the rainbow colored artifact. The depth information and horizontal location of the image is stored entirely in the orientation of the fringes.

What if the fringes were spaced MUCH more widely than the wavelength of the illuminator? If we double, or triple, or quadruple the fringe spacing of the interference pattern, THE HOLOGRAM STILL WORKS. If we convert each fringe into an independent macroscopic line scatterer, the hologram still works. Very strange. And it leads to something wonderful. If the following pattern was scratched by hand into a sheet of plastic:

Fig. 2 Make this scratch pattern on plastic

...it would create a little glowing dot which floats inside the plastic as a virtual image. It would be a "single pixel" Rainbow Hologram, but with absolutely gigantic interference fringes. They wouldn't even be interference fringes anymore, and optical interference would no longer apply. Yet the hologram would still function, it would still reconstruct a 3D scene. Holography without interference. (Pretty easy to generate with a computer, eh? Hint hint!)

To recap, here is what we do: we take the "single pixel" stripes of a Benton Rainbow hologram, square off the sinusoidal fringe pattern, increase the distance between the fringes by several orders of magnitude, and lower their duty cycle so they appear as single thin lines with wide spaces between them.

Fig. 3 Progressively simplified Rainbow Hologram zoneplates

In terms of interference, we would find that the "rainbow" artifact we see in these holograms would acquire numerous overlapping copies of itself (each caused by higher-order beams produced by the square, nonsinusoidal fringes.) As the fringe spacing was enlarged, the multiple copies of the rainbow stripe would compress together into a single glowing stripe of apparently white light. The "rainbow" would be gone, it would have turned white, yet the rest of the hologram still functions as it originally did, it still creates the same 3D scene.

Another person points out that "scratch holograms" cannot reconstruct opaque objects, therefore they are not true holograms. Wrong! Scratch- holograms employ the same geometry as genuine Rainbow holograms and they have no trouble with opaque objects. Opacity is created by removing certain portions of the zoneplate interference patterns (or portions of the curved scratch.) I've drawn images of black opaque objects against deeper objects, and images of transparent apertures in opaque plates which reveal larger, deeper images seen through the "hole." Note the upper hologram in the following photo, where an opaque black square floats above a deep plane of glowing dots. There's a trick to it, but Benton's holograms employ exactly the same trick.

In addition, a scratch-hologram can produce conjugate or "pseudoscopic" images. Rather than lighting your scratch-hologram from above, light it from below. The image will appear... but it will be inside out! If your image was designed to float deep inside the plastic plate, now it will be hovering in the air in front of the plate. A conjugate illumination beam will convert a virtual image into a real image whether you're working with conventional holograms or "scratch-holos."

Also, a scratch-hologram can function in transmission mode as well as reflection mode, just like a conventional hologram. If you use clear plastic rather than black plastic, you can place your hologram between your eyes and a distant light source, then find the holographic image.

The particular geometry of Rainbow holograms allows anyone to draw the fringe patterns by hand with a needle, and to thereby create "holographic" images without lasers and even without interference. This can be taken to ridiculous lengths: giant "holograms" composed of curved, polished metal rods become practical. The metal rods are the interference fringes! Or imagine huge sheets of vacu-formed silvered plastic; like greatly enlarged foil holograms taken from your credit card.

It is not strictly necessary that the above horizontal swatch of interference pattern be exactly duplicated in order to produce a hologram. When the fringes have been widely separated they stop interacting, so an individual "fringe" can replace the multiple-fringe pattern. A conventional hologram's pattern of nested hyperbolic fringes can be replaced with a single curved reflective fiber or surface scratch. It need not even have a hyperbolic shape. If some vertical and depth distortions can be tolerated, then a circular scratch drawn with a compass makes a dandy "hologram diffraction grating."

I've been drawing holograms of numerous simple 3D objects by scratching a polished plastic plate by hand with a compass. The X,Y position of the scratches determines the X,Y position of the reconstructed image points, and the radius of each scratch determines the perceived depth of the image point. It's akin to needlepoint knitting, since images must be built up from hundreds of brightly glowing dots. It takes quite a bit of labor to produce a simple image such as a piece of holographic text, or a 3D polyhedron.

So far I've drawn such things as polyhedra, starfields, text at various depths, opaque planes which hide text behind them, boxes with walls composed of random dots, etc. When lit with a nearby extended source these "holograms" appear as sets of fine curved scratches, somewhat like several superposed LP record albums. When illuminated by a distant point-source, each scratch produces a small "highlight," and the whole set of scratches produces a 3D object composed of bright highlight points.

See, scratch holograms ARE real holograms. Nyaa-nyaa, tol ya so!

BUT ARE THEY REALLY?

Other writers point out that "scratch holograms" are like conventional photographs in that the film-plate itself does not preserve the phase of the illuminating light source, and therefore they are not holograms. This is wrong: the polished scratches do preserve horizontal phase information. Remember that mirrors preserve the phase of reflected light. So also do the interference patterns of conventional Rainbow holograms. So do cylinder lenses and shiny fibers. And so do the polished scratches of "scratch holograms". Eliminate the phase by painting the scratches white, and you also eliminate the 3D depth effect. True, "Scratch holograms" are astigmatic, preserving the horizontal phase (and the horizontal parallax) while scrambling the vertical phase. Each scratch in a "scratch hologram" acts as a tiny cylindrical mirror, and it reflects light like a flat mirror in one dimension while scattering light in the other. As a result, both rainbow holograms and "scratch holograms" only have horizontal parallax, and the 3D effect will vanish if they are turned sideways. Their horizontal parallax depends upon their ability to preserve horizontal spatial phase of the illuminating light source. It's like looking into a curved, slit-shaped mirror. We see a virtual image of the illuminating source formed by the curved mirror, and since the illuminator is a point source, we see a glowing dot which floats either behind or before the plastic surface.

STILL NOT TRUE HOLOGRAMS

The cause is simple: if we "rubber stamp" some single-pixel holograms onto a recording medium, we do not create a hologram of a multi-pixel object. The scratches interact (overlapped scratches destroy one another.) In true holography the light waves add linearly, and one wave does not block the effects of another. "Stamping" of complete zoneplate patterns onto the plastic is not an additive process as it would be with light. However there is a cure: divide the film-plane itself into pixels, then move any overlapping scratches within each pixel so they no longer overlap, but so they do not alter the 3D image by moving outside their pixel boundaries. This allows the "scratch-holo" technique to reproduce arbitrary scenes, rather than only being used for glowing white lines on a dark background.

BUT ARE THEY HOLOGRAMS? The answer is a matter of opinion. Some people don't regard Rainbow holograms as true holograms either. These "scratch holograms" are even further away from the original off-axis holographic technique of the 1960s. Yet they do include the arrays of line-scatterers which all holograms exhibit. And they do rely on coherent reflection of an illumination beam, and so they absolutely require point-source illumination, and cannot be used with extended light sources. Use of extended-source illuminators causes severe depth-blurring in every sort of holographic recording. Simply because "scratch-holos" suffer from the same unique limitations as conventional holograms, that alone is enough to declare them to be truly holographic.